MobileNets v2
MobileNetV2-反向残差和线性瓶颈
MobileNetV1 中解读了深度可分离卷积,这里不做赘述。在 MobileNetV2 中增加了两个概念(idea) : Linear Bottleneck 和 Inverted Residuals。
不错的解读:
一些理解:
- 因为 ReLU 导致信息丢失,所以使用了 Linear bottleneck
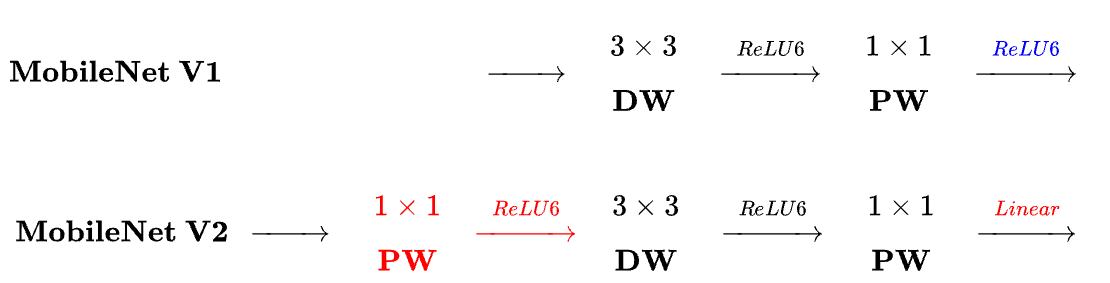
- MobileNetV1: depthwise + pointwise
- MobileNetV2: pointwise + depthwise + pointwise
- 几张图
Preliminaries, discussion and intuition
Depthwise Separable Convolutions
深度可分离卷积是许多高校神经网络架构的关键构建模块,本文也使用了这个。深度可分离卷积的基本思想就是用分解后的卷积算子替换原先的完整卷积,将卷积分成了两个独立的层。第一层为深度卷积,就是对每个输入通道进行了一个轻量化的滤波。第二个是$1\times 1$卷积,即点态卷积,用来将输入通道进行线性组合。
标准的卷积输入张量 $L_i(h_i\times w_i\times d_i)$, 通过应用卷积核 $K \in R^{k\times k \times d_i \times d_j}$ 产生一个 $h_i \times w_i\times d_j$ 的输出张量$L_j$,标准的卷积层的计算代价为 $h_i\times w_i \times d_i \times d_j \times k \times k$,
深度可分离卷积是标准卷积的直接替换,他和常规卷积性能相近,但代价只有 $h_i \times w_i \times d_i (k^2 + d_j)$,即两部分的代价和。与传统卷积层相比它有效的减少将近 $k^2$ 的代价。MobileNetV2 使用了 $k=3$ 的深度可分离卷积使得卷积代价是标准卷积的 $1/8\sim1/9$,精度只会有一点的降低。
这一方面可以在 MobileNets1中查阅。
Linear Bottlenecks
对于一个 $n$ 层的深度神经网络,每一层 $L_i$ 都有一个维度为 $h_i \times w_i \times d_i$的激活张量,(这部分主要说明这个激活张量的一些基本性质),这可以看成一个含有 $h_i\times w_i$ 个 $d_i$ 维“像素”的容器。非正式地说,对于来自真是图像的输入集,可以说层激活体(对于任意层 $L_i$ )形成了一个“兴趣流形”。长期以来,一直假设神经网络中感兴趣的流形可以嵌入到低纬度的子空间中。换句话说,对于深度卷积层钟的所有独立的 $d$通道像素,编码在这些值中的信息实际上位于某些流形中,而这些流形则又可以嵌入到一个低维子空间中。
这种事实,可以通过简单地减少层的维数来获知和利用,并从而减少操作空间的维数。 MobileNetV1 利用了这一点,并通过一个宽度乘法因子有效的在计算量和精度之间进行权衡,并将其纳入其他网络中以及 ShuffleNet 中。根据这种直觉,宽度乘法因子允许人们减少激活体空间的维度,直到兴趣流体跨越整个空间。(意思就是说,假设激活体维度为 $M$, 实际上主要信息只需要 $m$ 维就可以,因此可以不断降低 $M$ 直到 $m$?)但是这种直觉似乎有点问题,因为深度神经网络中实际上都是使用的非线性的坐标变换。例如 ReLU。例如在 $1D$ 空间中对线使用 ReLU,则会产生一条射线。在 $n$ 维空间内使用,则会产生一个具有 $n$ 节点的分段线性曲线。
很容易的看出,如果有一层的变换 $ReLU(Bx)$ 的输出中含有一个非零体 $S$,那么 映射到 $S$ 内部中的点是通过一个线性变换获得的,也就是说,对于整个维度的输出空间,对应的输入空间的部分,是与线性变换控制的。(不好表达文章的意思,意思是说,对于输出 $M$ 维的中的非零体 $M^{\prime}$, 输入中的 $m$维,只有其中经过线性变换的 $m^{\prime}$ 部分有关,也就是说,线性变换 $B$ 决定了相关的输入,不然的话,非线性例如 ReLU,就会把一部分信息丢掉,比如 Relu 中 x < 0)。换句话说,深度网络仅对非零体部分具有线性分类器的能力。
另一方面,当使用 ReLU 塌缩通道时,它不可避免地会导致这个通道的信息丢失。然而,如果有很多通道的时候,激活流形中可能有一个结构,其他通道的信息存储在其中。如果输入流形可以嵌入到激活空间的显著低维子空间中,那么 ReLU 变换将会在将所需的复杂性引入可表达函数集的同时保留信息。
总结来说,兴趣流形位于高维的激活空间中的低维子空间中:
- 如果兴趣流形在 ReLU 后保持非零,那么它对应线性变换。
- 只有输入流形位于输入空间的低维子空间中时,ReLU 才能保留输入流形的完整信息。
这对优化现有的神经网络架构进行了提示:假设兴趣流形是低维的,那么就可以通过在卷积块中添加 Linear bottleneck 层来获取它。实验表明使用线性层是重要的,这可以防止非线性破坏太多的信息(后续的实验证明了缺失会降低性能,还有一些工作,例如论文中提到的CIFAR数据集)。后面会使用 bottleneck convolutions,把输入瓶颈的大小和内部尺寸的大小的比例称为膨胀比。
Inverted residuals
bottleneck 块类似 residual 块,每个块包含一个输入,后面是一些 bottleneck,然后是深度残差网络中的扩展块。因为 bottleneck 中包含了所有必要的信息,而扩展层仅仅作为一个实现细节伴随非线性的张量变换,因此在 bottleneck 中使用了 shortcurts。
Running time and parameter count for bottleneck convolution
基本实现结构如下所示:

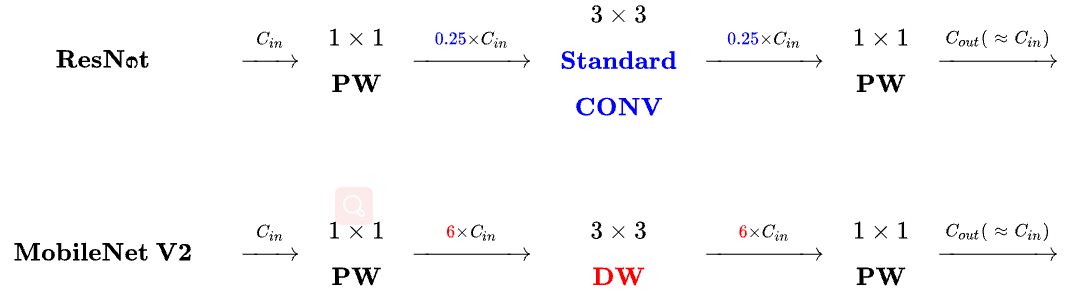
对于一个大小为 $h\times w$ 的块,扩展因子为 $t$,核大小为 $k$, 输入通道数为 $d^{\prime}$, 输出通道数为 $d^{\prime\prime}$。总共的乘加计算为 $h \cdot w \cdot d^{\prime} \cdot t(d^{\prime} + k^2 + d^{\prime\prime})$。表达式中有一个额外的项,因为有一个额外的 $1\times 1$卷积,但是网络的性质允许使用更小的输入和输出维度。不同分辨率下的 MobileNetV1, MobileNetV2, ShuffleNet 对比如下。
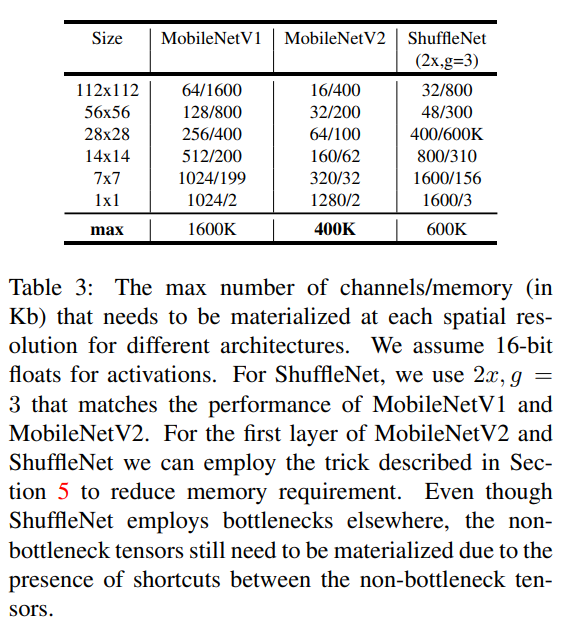
略略略
Implements Notes
Memory efficient inference
反向残差瓶颈层允许特别的内存高效实现,这对移动端应用非常重要。使用例如TensorFlow或者Caffe的一种标准高效的推理实现方式,是通过构建一个有向无环的计算超图 $G$,由表示操作的边和表示中间计算张量的结点组成。计算被安排进行时为了最小化存储在内存中的张量的总数。在一般的情况下,它搜索所有可能合理的计算顺序 $\sum(G)$,并且选择其中最小化下式的一项:
其中 $R(i,\pi,G)$ 为中间张量的列表,这些张量与 $\pi_i…\pi_n$中的结点连接。$|A|$ 代表张量 $A$ 的大小,$size(i)$ 代表操作 i 期间内部存储所需要的内存总量。
对于只有平凡平行结构的图(例如残差连接),只会由一个非平方可行的计算顺序,因此基于计算图 $G$ 的推理所使用内存总量和上界则可以简化为:
或者重新说明一下,内存的总量就是所有的输入和输出(combined)的总大小的最大值。如果把 bottleneck residual block看作一个单独操作,并且将内部的卷积看作是可丢弃的张量,那么内存的总量将由 bottleneck 张量的大小决定,而不是 bottleneck 的内部张量的大小(更大)。
BottleNeck Residual Block
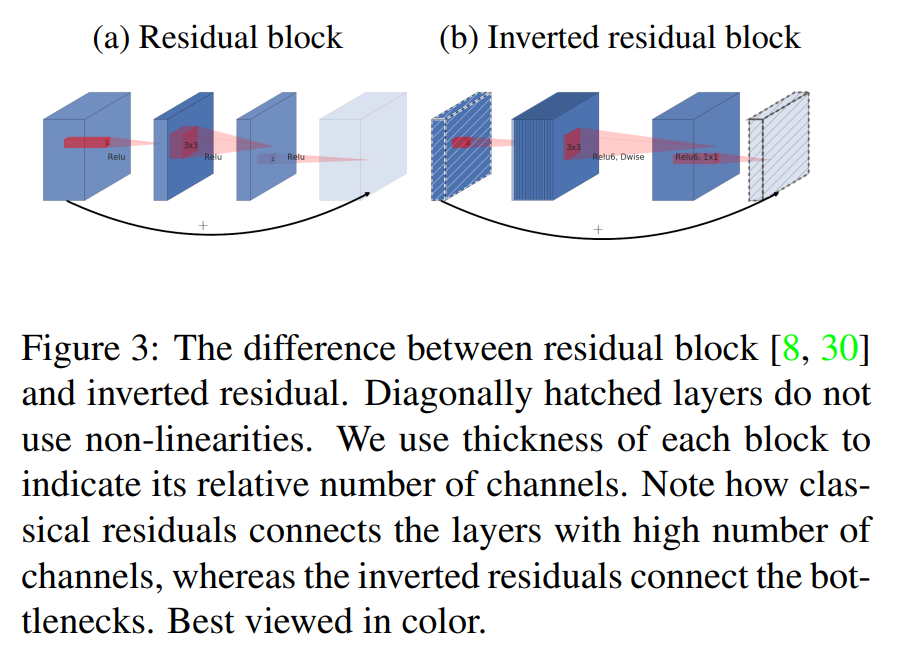
如上图中的(b),瓶颈块操作 $\mathcal{F}(x)$可以表达为三个操作的组合 $\mathcal{F}(x)=[A\circ \mathcal{N} \circ B]x$。在这里,
- $A$ 为线性变换 $A: \mathcal{R}^{s\times s\times k} \rightarrow \mathcal{R}^{s\times s\times n}$.
- $\mathcal{N}$ 为一个非线性的逐通道的变换 $\mathcal{N}: \mathcal{R}^{s\times s\times n} \rightarrow \mathcal{R}^{s^{\prime}\times s^{\prime}\times n}$
- $B$ 又是一个到输出域的线性变换 $B: \mathcal{R}^{s^{\prime}\times s^{\prime}\times n} \rightarrow \mathcal{R}^{s^{\prime}\times s^{\prime}\times k^{\prime}}$.
在本文的网络中,$\mathcal{N} = $ ReLU6 $\circ$ dwise $\circ$ ReLU6,但是结果适用于任何逐通道的变换,假定输入域大小为 $|x|$,输出域大小为 $|y|$,那么计算 $F(X)$的需要的内存将会低至 $|s^2k|+|{s^{\prime}}^2k^{\prime}|+O(\max(s^2,{s^{\prime}}^2))$
算法基于一个事实,内部张量 $\mathcal{I}$ 可以表示为 $t$ 个张量的连接,每一个大小为 $n/t$,那么函数就可以表示为:
通过累加和,则只需要在所有时刻,只在内存中保存一个大小为 $n / t$ 的中间块。如果 $n = t$,则在所有时刻只需要保留内部表示的一个通道即可。(所以是整体计算变成了滑动计算的意思?)
可以使用这个技巧的两个约束条件:
- 内部变换(包括非线性和深度)是逐通道的
- 连续的非逐通道的操作需要输入和输出的比率显著
对于大多数的传统神经网络,这样的技巧不会产生显著的改进效果。
使用 $t$ 分割的方式来计算 $F(X)$ 的Multi-adds操作数与 $t$ 独立,但是在现在的一些实现中,使用较小的矩阵来替换乘法会损害运行时,这是因为缓存丢失的增加。这种方法最只用于 $t = 2\sim 5$ 的小常数。它显著降低了内存的需求,但仍然允许使用深度学习框架提供的高度优化的矩阵乘法和卷积算子获得的高效率。框架级别的优化是否可以带来进一步的运行时优化仍待研究。