SCV

代码已开源

RAFT outperforms other approaches by first calculating all-pairs similarity and then performing iterations at a high resolution.The price is that it inurs significantly larger computation burden.(FastFlowNet)

Abstract

SOTA的光流估计网络需要高分辨率下的稠密的Correlation Volume来衡量逐像素的位移，虽然稠密的Correlation Volume有助于准确的光流估计，但是繁重的计算和内存使用也不利于模型的训练和部署。这篇论文说明了稠密的Correlation Volume表示是冗余的，只需要其中的一小部分元素就可以实现精确的光流估计。在此基础上，论文提出了一个可以替代的位移表示方法—Sparse Correlation Volume，通过直接计算fmap1在fmap2上最接近的k个匹配来构建，并存储在一个稀疏的数据结构中。实验说明了该方法可以显著降低计算成本和内存占用，并且依然保持较高的精度。

Introduction

基于直觉：img1的某一个特征向量只会与img2的某一部分特征向量高度相关，因此在稠密的Correlation Volume表示中，会有大量的冗余，对于相关度较小的特征并不会优化预测结果。如下图所示。

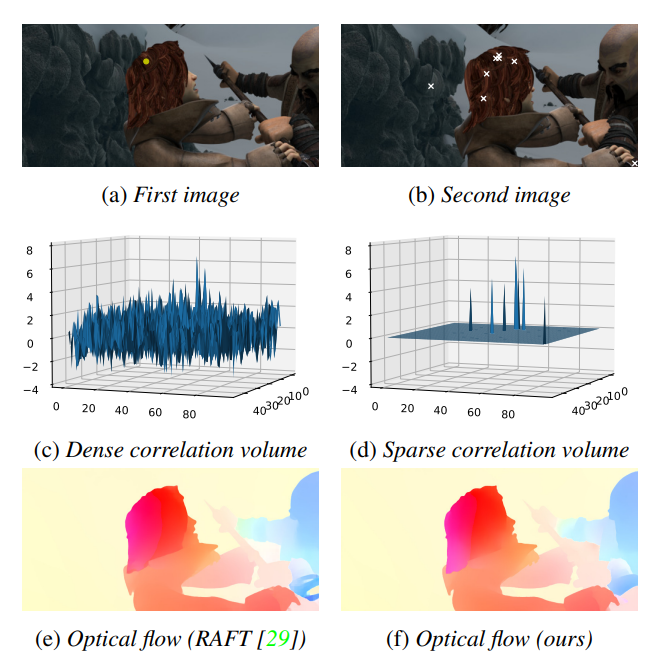
论文提出了Sparse Correlation Volume 表示，只有每个像素的top-k的相关值会被存储在稀疏数据结构中，就是个键值对—（{value, coordinates}）。

Method

记 $I_1, I_2: \mathbb{Z}^2 \rightarrow \mathbb{R}^3$ 为两张RGB图像，待解决的问题就是估计稠密的流场 $f:\mathbb{Z}^2\rightarrow\mathbb{R}^2$，映射每个像素x到其位移向量$f(x)$。

现在的深度学习光流估计方法，首先会对图像对进行特征提取得到图像的feature map $F_1,F_2:\mathbb{Z}^2\rightarrow\mathbb{R}^c$，这里的 $c$ 为通道数，Correlation Volume $C : \mathbb{Z}^4 \rightarrow R$ 由特征向量直接的点积得到。

$$C(x,d)=F_1(x)\cdot F_2(x + d).$$

输出为一个四维的张量，可以表示为集合:

$$\mathcal{C}=\{C(x,d)|x\in \mathcal{X}, d \in \mathcal{D}\}.$$

这里， $\mathcal{X} = [0, h
) \times[0, w) \cap \mathbb{Z}^2$ 为 feature map $F_1$ 的域， $|\mathcal{X}| = hw$ ，其中的 $h$, $w$ 分别为 $F_1$的 $height$ 和 $width$。$d$ 为 $x$ 方向或者 $y$ 方向上的最大位移量，并且有 $|\mathcal{D}| = (2d+1)^2$，因此，Correlation Volume $\mathcal{C}$ 中含有 $hw(2d+1)^2$的元素。

为了降低Correlation Volume的尺寸，以前的方法使用了由粗到细的策略，然后对有限的d进行warping操作，为了精确处理大位移的问题，RAFT构建了全局的Correlation Volume，当然，位移的范围d受到feature map的大小限制。RAFT的Correlation Volume包含了 $N^2$ 的元素，这里的 $N = hw$。论文中将空间复杂度从 $O(N^2)$ 降低到了 $O(Nk)$，具体 如下图所示。

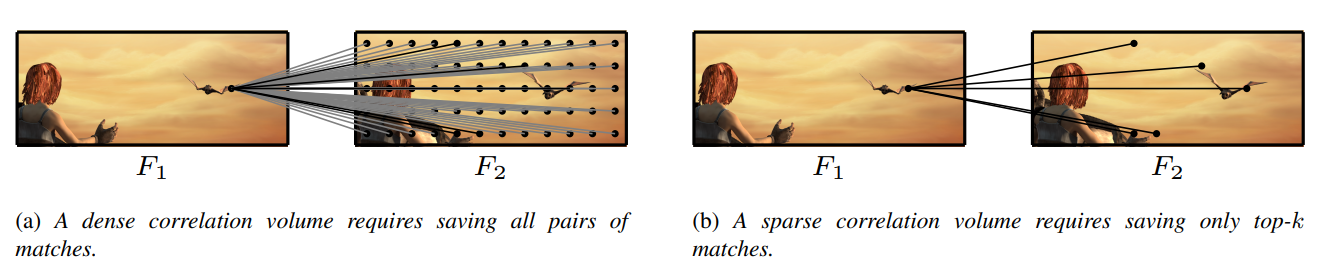
Sparse Correlation Volume

对于 $x\in \mathcal{X}$, 定义集合 $S_x^{(k)}$包含 $k$个产生最大相关值的位移:

$$S_x^{(k)} = {\arg \max}_{S \subset \mathcal{D},|S|=k}\sum_{d\in S}C(x,d)$$

则Correlation Volume可以表示为一个四维的稀疏张量:

$$\tilde{\mathcal{C}}=\{C(x,d)|d \in S_x^{(k)},x \in \symcal{X}\}.$$

这样的稀疏Correlation Volume则只包含 $hwk$ 个元素，而原来的则包含 $h^2w^2$ 个元素， 常数 $k$ 通常为一个比较小的数，例如8。网络结构如下所示。

k-Nearest Neighbours

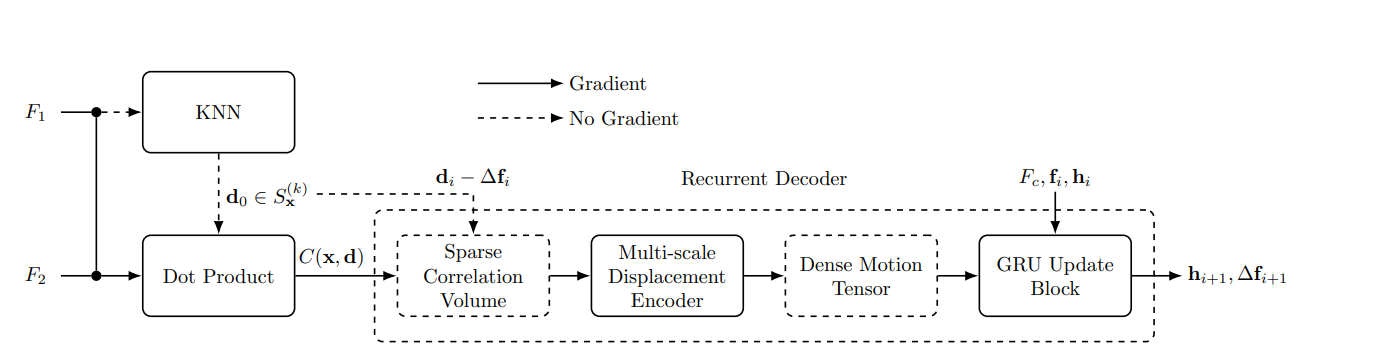
使用了两个共享权重的提取网络从输入的图像中获取 1/4 分辨率的特征图。特征提取网络包含了 6 个 residual blocks，特征通道数为 256。为了构建稀疏Correlation Volume，使用了一个 KNN 模块(论文中有参考文献)去计算对于 $F_1$的每个特征向量的最大的 $k$ 个相关得分的索引集合。稀疏Correlation Volume通过 $F_1$ 的每个特征向量与 $F_2$ 由索引得到的前 $k$ 个特征向量的点积。在back-propagation阶段，梯度也仅会传到由 KNN 模块选择到的 k 个特征向量。

Displacements Updates

采用了全局的迭代精化方法，估计残差流可以有效的减少搜索空间并且可以比直接回归预测到更好的结果。与直接预测光流场 $f$ 不同，残差流 $\Delta f_{i+ 1}$ 是每一步预测并且用来更新当前的光流估计结果 $f_{i + 1} = f_i + \Delta f_{i + 1}$。

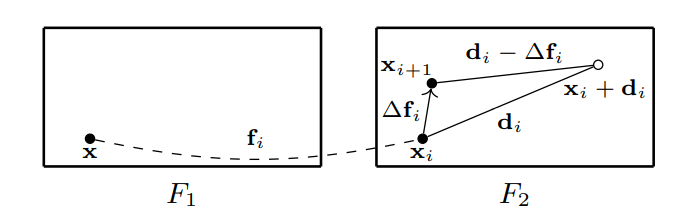
在每一步，对于 $F_1$ 的一个像素 $x$，将会根据当前的光流预计结果映射到 $F_2$ 中的 $x_i = x + f_i$。稀疏Correlation Volume可以看成初始光流$f_0 = 0(i = 0)$。当坐标$x_i$更新到$x_{i+1}=x_i+\Delta f_i$， $\tilde{\mathcal{C}}$中对应的位移也会同样更新。可以通过在每一步中从 $d_i$ 中减去 k 最近的 $\Delta f_i$ 来shift稀疏Correlation Volume张量的坐标，$C_i(x,d_i)=C_{i+1}(x,d_i - \Delta f_i)$。 如下图所示。并且设定为$d_i-\Delta f_i$为浮点值。需要注意的是，内积只会在最开始的时候计算一次，因为在每一步中，只有相关坐标发生变化，相关值不会发生变化。

Multi-scale Displacement Encoder

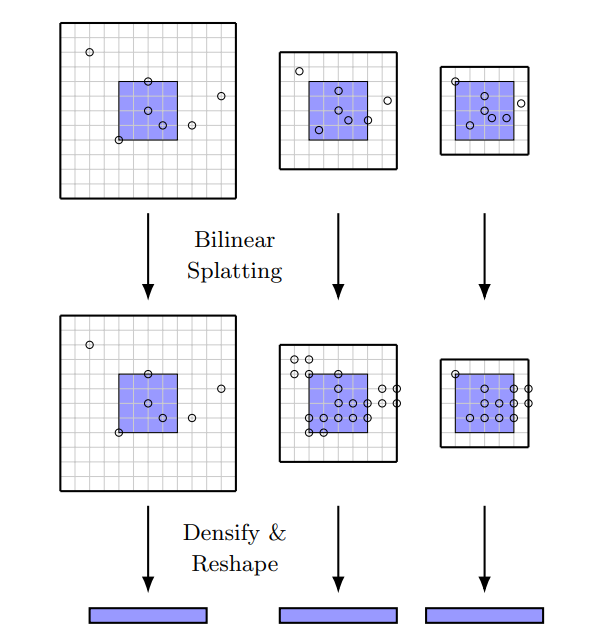
在多个分辨率下以固定的半径创建多尺度的稀疏张量和采样位移，粗糙的分辨率将会提供更大的文本背景，而精细的分辨率则可以提供更精确的位移。然后将每一个 level 的稀疏张量转换为稠密张量并 concatenate 形成一个 2D 张量.如下图所示。

在每一次迭代时，对于每个像素 $x$，从 $top-k$ 个相关位置$S_x^{(k)}$ 开始 ，因此集合 $\{(d,C(
x,d)|d\in S_x^{(k)}\}$ 记录了对于 $X$的 $top - k$ 个相关值及其位置，这通过 $kNN$ 算法得到。

构建了一个5层的稀疏Correlation Volume金字塔通过以（1，2，4，8，16）除坐标(意思就多分辨率的图像？)，并且表示在level l 的 比例化位移，通过当前的流 $\Delta f_i$ 更新的结果为 $d^l=(d_i-\Delta f_i)/2^{l-1}$。

此外，在level l的相关值表示为 $C^{l}(x,d^l)=C(x,d)$ 对于 $d\in S_x^{(k)}$。在每一个level，通过常数半径 $r$ 限制了位移范围，并且定义level l的窗口相关值集合为:

$$\{(d^l,C^l(x,d^l)) \mid ||d^l||_{\infty} \leq r, d\in S_x^{(k)}\}.$$

因为坐标 $d^l$ 不一定是整数，所以需要重采样到整数坐标以稠密化 correlations的稀疏张量。文中提出了一种叫做”bilinear splatting“的方法，相关值将会被 bilinear splat到四个最近的整数网格中。例如， 在位置 $d^l$ 的相关值 $C^l(x,d^l)$将会被传递到四个邻近整数点的每一个，用 $[d^l]=(d_x,d_y)$ 表示，根据下式:

$$C^l(x,[d^l])=(1-|d_x^l-d_x|)(1-|d_y^l-d_y|)C^l(x,d^l)$$

这些值将会累加对于(5)中的集合，每一个 level 的稀疏张量也会传换成稠密张量，reshaped 并 concatenate 成一个 2D 稠密张量维度为 $5(2r + 1)^2$，这里 5 为金字塔的层数。

这个方法不含可学习参数，仅仅是稠密到稀疏张量的转换，并且比稀疏卷积容易。

GRU Update Block

concatenate 2D 运动张量，上下文特征和当前的光流估计结果，并将结果传到GRU单元中，GRU单元将会不断更新估计残差流 $\Delta f_{i+1}$，这个将会在下一步中用来 shift Correlation Volume的坐标。

Experiments

Implementation details

Network details

首先提取 1/4 分辨率的256通道的特征图，特征提取网络包含了 6 个residual blocks。当特征图传到 $kNN$ 时，设定了 $k = 8$。也就是说，对于每个特征向量，将会返回可以得到最大内积的 $top-8$ 个特征向量的坐标。GRU 单元将当前的光流估计和上下文特性图作为输入，上下文特征图由128通道的独立网络获取。GRU 单元将会更新128维度的隐藏层特征向量。在训练阶段，GRU 将会迭代8次（RAFT 迭代12次）。

Training schedule

(1, 2) pre-train

(3, 4, 5) fine-tune

次序	数据集	batch-size	迭代次数
1	FlyingChairs	6	120k
2	FlyingThings	4	120k
3	Sintel	4	120k
4	KITTI	4	50k
5	HD1K	4	50k

Training: 2 $\times$ 2080Ti GPU

Ablation experiment: 1 $\times$ Tesla P100 GPU

Loss function

与 RAFT 一样，使用了循环网络结构预测一系列的残差流 $\Delta f_i$, 每一个阶段的光流预测结果可以表示为 $f_{i+1}=f_i+\Delta f_{i+ 1}$，初始值 $f_0 = 0, \Delta f_0 = 0$。

损失函数针对于光流预测的序列结果，对于给定的真值光流 $f_{gt}$，对于每一阶段的预测结果 $f_i$,损失函数定义为:

$$L = \sum_{i = 1}^N\gamma^{N - i}||f_i-f_{gt}||_1$$

权重因子: $\gamma = 0.8$（pre-train on Flyingchairs + FlyingThings), $\gamma = 0.85$ (fine-tune on Sintel and KITTI)

总阶段数: $N = 8$

kNN

使用了 faiss 库在 GPU 上跑 $kNN$，具体参考论文以及对应的参考文献。非常的amazing。

Results

定量分析结果如下表所示。

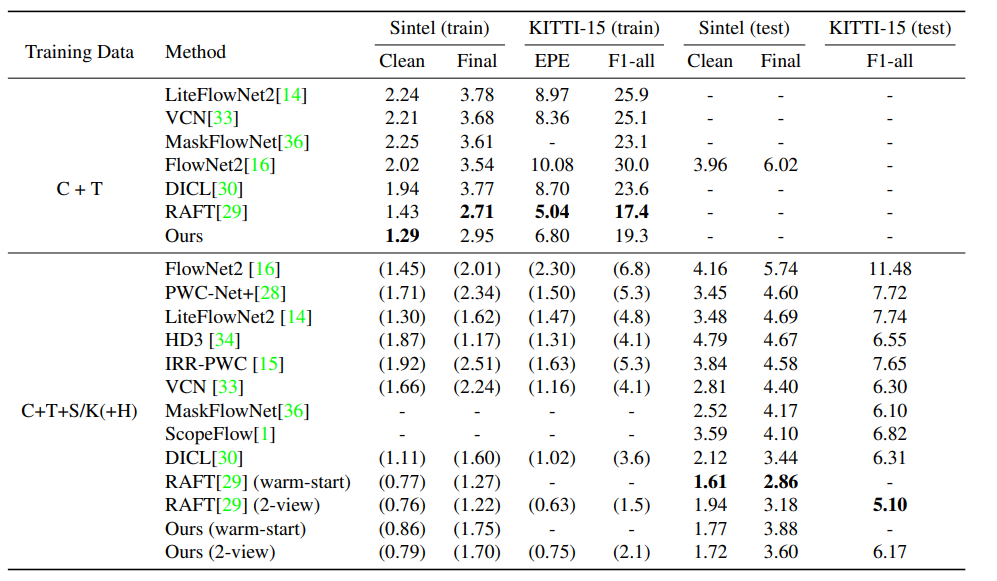
Sintel Clean数据集从RAFT的 1.94 改进到了 1.72 。同时测试了RAFT的 warm-start 策略（用前一帧的光流估计结果初始化当前的光流估计结果）。这个策略没有改进本文的模型，仍然落后于RAFT(warm-start)。在 Sintel 数据集上，模型和 SOTA 相差不大，只比 RAFT 和 DICL 差了一点。同时测试了预训练模型 (C+T) 在 Sintel 和 KITTI-15 上性能，在Sintel Clean 达到了最好的性能，在 Sintel final 和 KITTI-15 上仅次于RAFT。

在 Sintel Clean 数据上的改进可以归功于较大的 Correlation Volume(1/4 分辨率 vs 1/8 分辨率)。量化结果如下图所示,很好的说明了在高分辨率下构建 Correlation Volume 和 进行光流预测的优势。

在Sintel Final 和 KITTI-15 数据上，存在比较大的运动模糊和特征缺失区域，因此 $k= 8$ 与稠密 Correlation Volume 相比就显得很小而不能达到同样的效果。后面的消融实验中也对 $k$ 做了分析。但是可以说明，尽管在所有的数据集上没有超过RAFT, 但是可以说明稀疏的方法，尽管只有很少的相关值，仍然可以得到不错的效果。对于每个像素，只需要存储 $k = 8$ 个相关值，但是 RAFT 却需要存储 $h\times w$ 个相关值，限制了向更高分辨率 scale 的能力。

Ablation

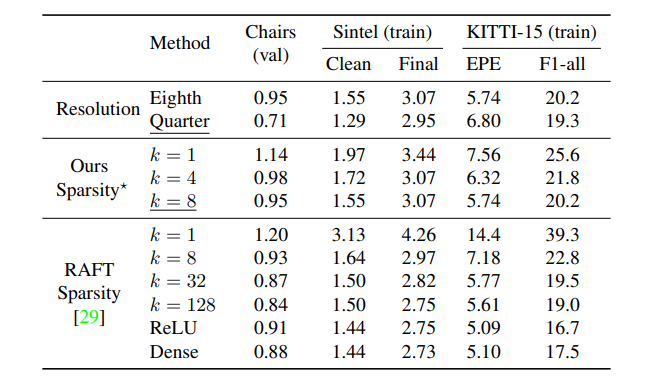
消融实验仍然是为了说明 $top-k$ 个相关值对于 full correlation volume来说是足够的。在 $1/8$ 分辨率下，更大的 $k$ 可以带来更好的结果，即便 $k = 1$ 与不会彻底失败。

同时比较了 $1/4$ 分辨率和 $1/8$ 分辨率，可以看出 $1/4$ 分辨可以达到更好效果，除了在 KITTI-15的 EPE 指标上。

同时对 RAFT 的原生实现进行了实验，保留了 Correlation Volume 中的前 $k$ 个，而对其他的设为 0，依次修改 $k = \{1,8,32,128\}$。在表中，RELU 代表设置负值为0，只保留相关值中的正值。同时训练了原始代码，用 Dense 标记。可以看出更大的 $k$ 可以得到更好的结果，$k = \{32,128\}$可以达到与 Dense 相近的结果。这验证了文章的假设，稠密的 Correlation Volume 会有很大的冗余，有一个较大的 $k$ 值的稀疏 Correlation Volume同样可以达到很好的效果。

具体结果在 Results的表中。

Memory Consumption

稀疏 Correlation Volume 并不会引进新的学习参数，因此参数个数和 RAFT 是一样的。对于输入图片为 $436 \times 1024$ 大小的图片，在分辨率为 $1/4$ 和 $1/8$ 下的稀疏 Correlation Volume 的尺寸和大小如下表所示。

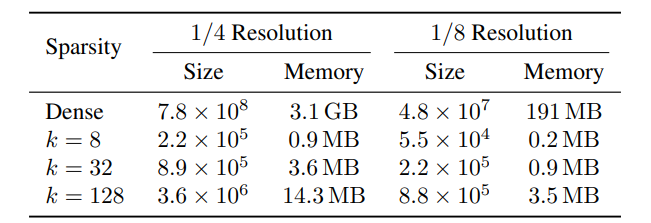
从 $1/8$ 分辨率下的特征图构建 Correlation Volume并不会带来内存的显著节省，这是因为 $kNN$ 库的常数 2GB消耗，Correlation Volume的内存消耗并不是瓶颈问题。

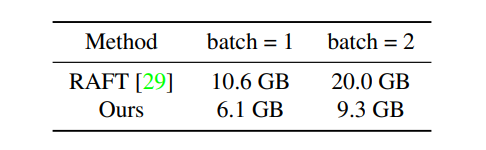
但是从 $1/4$ 分辨率下构建可以看出很清晰的优势，对原图片进行 $400\times 720$ 的随机切割，并且 $batch-size =1,2$ 可以看出该方法与 RAFT 相比可以将近 50% 的内存。

Limitations

简单的说就是，对于fine-strcture 的运动可以看出很大的改进，但是由于 EPE指标是考虑全局的，这是面向大区域的大尺度运动的偏差。这个方法的劣势在于对特征缺失或者模糊的区域。这些区域的特征因为模糊就需要很多的匹配，但是 $top-k$ 可能就不够充分去包含正确的匹配，并且会给出不正确的运动预测结果。一个失败的例子如下图所示。

Related Work && Conclusion

不做赘述.