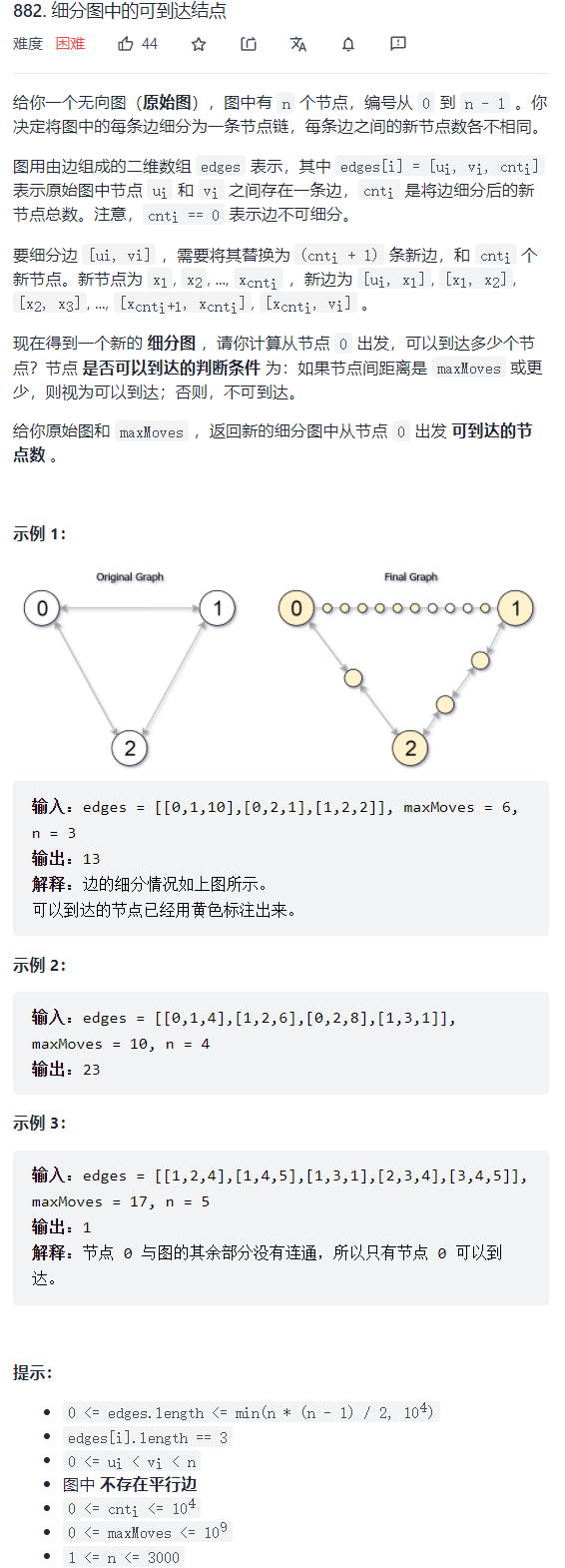
思路
dijkstra 求最短路, 可以分出 c 个点,等价于两点之间的路径长为 c + 1
求出最短路后,对每一条边进行遍历,则 $a \rightarrow b$中除了端点 $a$ 还可以遍历到 $min(c, maxMoves - dist[a])$ 个点(如果 $dist[a] < maxMoves$),记为 $x$ , 而 $b\rightarrow a$除了端点 $b$ 还可以遍历到 $min(c, maxMoves - dist[b])$ 个点(如果 $dist[b] < maxMoves$), 记为 $y$,则 无向边 $a \leftrightarrow b$,除了端点外还可以访问到 $min(x + y, c)$ 个点,对于原始的 $n$ 个顶点,若 $dist[j] \leq maxMove$,则 $j$ 可以访问到。累加所有即可。
AC code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| const int inf = 0x3f3f3f3f;
class Solution {
public:
vector<vector<int>> w;
vector<int> dist;
vector<bool> st;
int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
w.resize(n, vector<int>(n, inf));
dist.resize(n, inf);
st.resize(n, false);
for(auto e : edges){
int a = e[0], b = e[1], c = e[2];
w[a][b] = w[b][a] = c + 1;
}
dist[0] = 0;
for(int i = 0; i < n; i++){
int t = -1;
for(int j = 0; j < n; j++){
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t =j;
}
st[t] = true;
for(int j = 0; j < n; j++){
dist[j] = min(dist[j], dist[t] + w[t][j]);
}
}
int res = 0;
for(int i = 0; i < n; i++) res += (dist[i] <= maxMoves);
for(auto e : edges){
int a = e[0], b = e[1], c = e[2];
int t = 0;
if(dist[a] < maxMoves) t += min(c, maxMoves - dist[a]);
if(dist[b] < maxMoves) t += min(c, maxMoves - dist[b]);
res += min(t, c);
}
return res;
}
};
|












