Internal Covariate Shift & Normalization
Interal Covariate Shift
The term interal covariate shift comes from the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.
The authors’ precise definition is:
We define Internal Covariate Shift as the change in the distribution of network activations due to the change in network parameters during training.
In neural networks, the output of the first layer feeds into the second layer, the output of the second layer feeds into the third, and so on. When the parameters of a layer change, so does the distribution of inputs to subsequent layers.
These shifts in input distributions can be problematic for neural networks, especially deep neural networks that could have a large number of layers.
Batch normalization is a method intended to mitigate internal covariate shift for neural networks
简单的说,Interal Covariate Shift(后面简称ICS)是在网络训练过程中,由于前面层中的网络参数不断更新而导致的网络输入的分布不均匀的现象。网络层的序列化意味着后续网络的输入为前面网络的输入,而由于网络参数的更新,对于原始相同的输入,其经过每一层后的输出都会变化。
机器学习的一个重要假设就是数据的独立同分布(Independent and identically distributed,后面简称为iid),虽然这并不可能。即使做不到idd,实际上很多机器学习的算法,例如逻辑回归,神经网络以然可以在非iid的数据上训练得到不错的数据,但很明显,iid可以简化模型训练,加快训练和提升预测能力。对这个概念的理解可以参考统计机器学习中的Covariate Shift,从概率的角度上就是,条件概率相同,但边缘概率不同,甚至更难理解了。再赘述一句理解的话,网络加深,网络参数不断更新,经过多次线性或者非线性变化,对于其中的某一层(不要抬杠的选第一层),它得到的输入都不一样的,即便在第一层输入相同的数据,但是最终的分类标签却还是一致的,那么这些数据就不再是iid了。
这会导致一些问题:
- 前面的网络需要不断的适应新的输入数据,降低学习率
- 后面的网络的输入的变化可能导致前面的网络陷入饱和区,训练过早停止
- 既然每层的更新是会直接或间接影响到其他层的,那么每一层的学习策略就不能那么“随意”,应该非常的”谨慎“,实际上,这种”谨慎“也不是那么可控的。
Whitening
为了得到iid的数据,因此在数据送入模型之前,会经过数据预处理阶段,因此白化的目的就在于得到iid的数据。
- 去除特征之间的相关性—> 独立;
- 使得所有特征具有相同的均值和方差 —> 同分布
PCA就是一种典型的方法。PCA Whitening
Normalization
但是,白化的计算成本太高,于是有了normalization方法,可以简化计算过程,又可以使数据尽可能保留原始的数据表达能力。normalization这种方式,实际上并不是直接去解决ICS问题,更多的是面向梯度消失等问题,去加速网络收敛的。而且,均值方差相等与同分布不是一个概念。
Normalization Framework
通常的变换框架如上所示,实际上就是做了个shift和缩放转换到(0,1)正态分布,随后再进行reshift和rescale,最终转换成了 ($b$, $g^2$) 的分布。这里的reshift和rescale参数是可以学习的,而不是固定的(0,1),很显然,因为输入范围本身就不可能确定为(0,1),可学习的re参数也更符合底层的学习能力。
与白化相比,实际差距还是很大的。
Batch Normalization
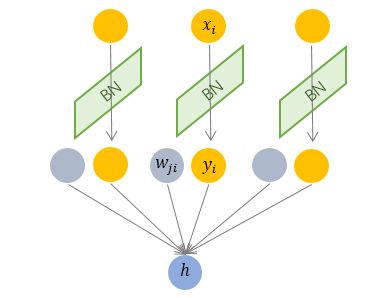
其规范化针对单个神经元进行,利用网络训练时一个 mini-batch 的数据来计算该神经元 的均值和方差,因而称为 Batch Normalization。

BN 可以看做一种纵向的规范化。由于 BN 是针对单个维度定义的,因此标准公式中的计算均为 element-wise 的。
BN 独立地规范化每一个输入维度 ,但规范化的参数是一个 mini-batch 的一阶统计量和二阶统计量。这就要求 每一个 mini-batch 的统计量是整体统计量的近似估计,或者说每一个 mini-batch 彼此之间,以及和整体数据,都应该是近似同分布的。分布差距较小的 mini-batch 可以看做是为规范化操作和模型训练引入了噪声,可以增加模型的鲁棒性;但如果每个 mini-batch的原始分布差别很大,那么不同 mini-batch 的数据将会进行不一样的数据变换,这就增加了模型训练的难度。
因此,BN 比较适用的场景是:每个 mini-batch 比较大,数据分布比较接近。在进行训练之前,要做好充分的 shuffle. 否则效果会差很多。
另外,由于 BN 需要在运行过程中统计每个 mini-batch 的一阶统计量和二阶统计量,因此不适用于动态的网络结构 和 RNN 网络。
Layer Normalization
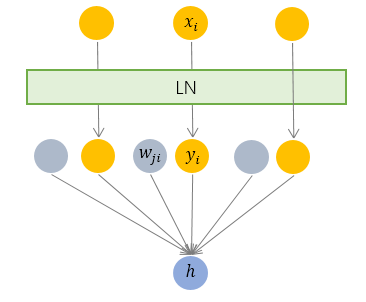
LN 针对单个训练样本进行,不依赖于其他数据,因此可以避免 BN 中受 mini-batch 数据分布影响的问题,可以用于小mini-batch场景、动态网络场景和 RNN,特别是自然语言处理领域。此外,LN 不需要保存 mini-batch 的均值和方差,节省了额外的存储空间。
但是,BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间,而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。
Instance Normalization
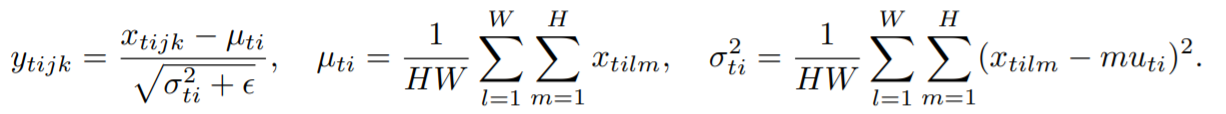
IN适用于生成模型中,比如图片风格迁移。因为图片生成的结果主要依赖于某个图像实例,更适合对单个像素有更高要求的场景。
Group Normalization
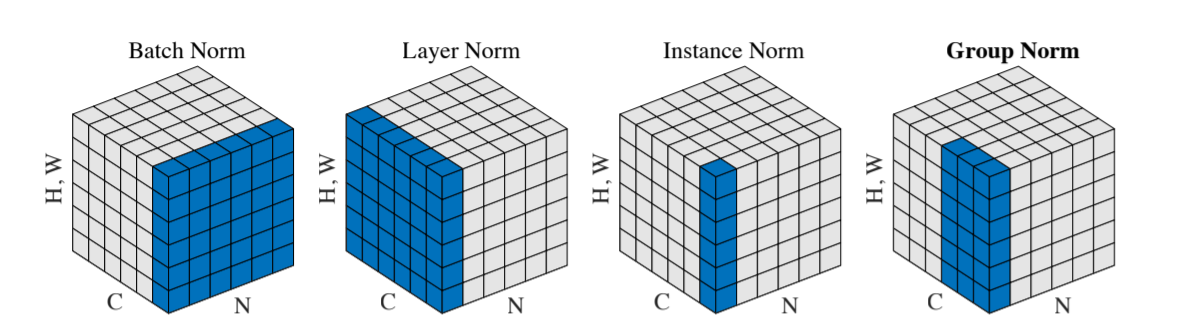
Kaiming He的论文中以图片的形式说明了四个的区别,Group介于IN和LN之间。
WN和CN跳过。
Normalizaiton的有效性可以参考文前的参考链接。





